About Problem

About Serial data

모든 “순서”가 있는 것들에서, “순서”란 중요한 정보이다. 이는 시계열만이 아닌, 우리가 말하는 문장에도 해당이 되는 말이다.

Transformer 이전에 자연어 처리에서 자주 사용했던 “RNN(Recurrent Neural Network)”의 경우, 이러한 “순서”대로 순환하며 순차적으로 입력을 받는 구조이다.
따라서, 우리는 이를 “Position-aware”하다고 말할 수 있을 것이다.

그러나, Transformer는 RNN과 같이 순차적으로 입력을 받지 않는다.

그렇다면, 우리는 어떻게 Transformer가 "순서"를 알고 이를 배우게 할 수 있을까?

Absolute Position Embedding(APE)

답은 생각보다는 단순하면서도 복잡하다. 단지, 위치를 표현하는 vector( $p_i$ ) 하나를 추가하여 기존의 token embedding에 더해주는 방식이다.
그렇다면, “우리는 어떻게 vector를 구성해야하나?” 라는 질문이 있을 수 있다. 그 질문에 대한 답이 “Sinusodial APE”와 “Learnable APE”이다.

Sinusodial APE

“Attention Is All You Need”; Transfomer의 시초가 된 해당 논문의 저자들은, Position Embedding을 추가하기 위해, sinusodial function을 아래와 같이 사용하였다.

\[\begin{cases} p_{i,2t} = \sin\!\left(\dfrac{k}{10000^{2t/d}}\right),\\[4pt] p_{i,2t+1} = \cos\!\left(\dfrac{k}{10000^{2t/d}}\right) \end{cases}\]

이때의 i는 입력받은 token의 index이고, t는 d-dimensional vector $p_{i}$ 에서의 특정 차원의 index이다. 즉, $p_{i,2t}$ 는 입력받은 token들 중 i번째의 token의 d-dimensional vector 중 $2t^{th}$ 의 element이다.

Learnable APE

위의, Sinusodial APE를 읽다 보면, 한 가지 의문이 들 것이다.

멋진 방법인 것은 알겠는데, 굳이? 그냥, positional vector 도 학습하면 안 되나?

그래서 “Attention Is All You Need”의 저자들은 해당 방법으로도 실험을 진행하기도 하였고, 이후 연구들에서도 데이터가 충분하다면 Learnable APE가 더 나은 성능을 보인다는 언급을 하였다. 따라서, Learnable APE를 사용한다면 성능도 좋으며 구현도 단순한 positional Vector를 얻을 수 있다.
물론, 이러한 Learnable APE의 성공은, task/data에 최적화된 “positional basis”를 학습했기에 성공했을 것이라는 믿음이 있다.

그렇다면, 왜 굳이 Sinusodial APE를 사용하는가? 라는 질문이 있을 수 있다. Sinusodial APE 또한, Learnable에 비해 아래와 같은 장점을 가지게 된다.

  1. Sequence Length Extrapolation에 강하다. (학습때보다 더 긴 길이의 토큰에도 positional vector를 계산할 수 있다.)
  2. 학습 파라미터가 0이므로, 잉여 모델 용량을 본체에 더 사용할 수 있음.

APE의 문제점

우리가 살펴본 2가지의 APE 모두 아래와 같은 문제가 있다.

  1. 길이 일반화 문제 Learnable APE와 Sinusodial APE 모두 추론(Inference)에서 길이로 인한 문제가 발생한다.

  • Learnable APE : Learnable APE는 학습시에 학습한 embedding lookup table을 바탕으로 Inference를 진행하게 된다. 그렇기에, Inference시에, 학습할 때 사용했던 max_length보다 더 긴 문자열(embedding lookup table 밖의 index)이 들어오면, 해당 index에 대한 positional vector를 만들어 낼 수 없다.

  • Sinusodial APE : Sinusodial APE는, 학습때보다 더 긴 길이의 입력에서도 positional vector를 계산할 수는 있다. 그러나, 모델이 그 길이를 학습하지 않았기에, 학습된 분포 밖으로 벗어나 성능이 떨어진다는 보고들이 있었다.

  1. 상대/거리 정보 문제 우리가 학습하고자 하는 Sequence는 순서를 가지고 있다. 절대적인 순서가 중요할 수도 있지만, 텍스트와 같은 Sequence에서는 문장내 구조적 관계나, 단어간 상대적 거리가 더 중요하게 작용한다.
    그러나, APE는 Sequence에서 나온 token 사이의 관계에 대해서 제공하지 않기에, 해당 관계는 Self-Attention으로 모델이 스스로 학습해야 합니다.

  2. Shift에 민감한 문제

(1) “I like CV”
(2) “Well, I like CV”

위의 두 문장은, 비슷한 뜻을 지니고 있다. 그러나, (2)는 (1)과 비교할 때, 앞에 하나의 토큰이 추가되었으므로, 그 뒤의 Absolute Position 자체가 바뀌게 되므로, positional vector가 모두 달라지게 된다. 위와 같은 shift가 누적되면, 성능이나 안정성에 크게 영향을 미치게 된다.

그렇다면, 우리는 이런 생각을 가질 수 있다.

Position을 Absolute Position으로 정하지 말고, 상대적인 위치 정보를 넣어주면 해결되는 것 아닌가?

Relative Position Embedding

위의 초기의 Relative Position Embedding들은 APE와 같이, 위치를 표현하는 vector( $p_i$ )를 token embedding에 더해주는 방식을 사용하게 된다.

또한, Self-Attention 구조에서는, Query와 Key를 연산하여 attention value를 얻게 됩니다. 그러므로, Relative Position Embedding은 Key - Query 사이의 거리에 대한 정보를 주입하는 것에서 시작한다.

이 논문에서 언급한 Relative Position Embedding들의 세부적인 구성에 대해서는 아래와 같다.

Self-Attention with Relative Position Representations

\[\begin{aligned} q_{m} = W_{q}x_{m} \\ k_{n} = W_{k}(x_{n}+\tilde{p}^{k}_{r}) \\ v_{n} = W_{n}(x_{n}+\tilde{p}^{v}_{r}) \end{aligned}\]

위의 논문은, 위의 식에서 시작한다. 식에서 $\tilde{p}^{k}{r},\tilde{p}^{v}{r} \in \mathbb{R}^{d}$ 은 학습 가능한 relative position embedding이며, 여기서 r 은 $clip(m-n,r_{min},r_{max})$ 으로 구성된다. ( $clip(m-n,r_{min},r_{max})$ 은, $r_{min}$ 보다 $m-n$ 이 작으면, $r_{min}$ 을 쓰고, $r_{max}$ 보다 $m-n$ 이 크면, $r_{max}$ 을 쓰고, 둘 다 아니면, m-n을 사용하는 방식이다 )

또한, 짐작하다시피, $q_{m},k_{n},v_{n}$ 은 각각 m,n위치에서의 query, key, value이다.

그렇다면, 위의 식은 곧, query의 위치 m과 연산 대상인 key의 위치 n을 고려하여 positional vector를 추가하는 방식인 것이다. 그러나, 이 방식은 $r_{min}$ 보다 가깝거나, $r_{max}$ 보다 멀면, 서로 영향을 미치지 않을 것이다라는 가정이 있다.

또한, Query에 positional vector를 추가하지 않음으로써, 다른 위치에 있는 query를 같은 attentive bias를 만들어 냈다. 이는, Position-invariant bias를 만들고, 불필요한 자유도를 줄였다.

Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context

\[q_m^Tk_n\]

이 논문은, 위의 수식을 분해하면서 시작된다.

\[\begin{aligned} q_m = W_q(x_m+p_m) \\ k_n = W_k(x_n+p_n) \\ \therefore q_m^Tk_n = (W_q(x_m+p_m))^TW_k(x_n+p_n) \\ = x_m^TW_q^TW_kx_n + x_m^TW_q^TW_kp_n + p^T_mW_q^TW_kx_n + p^T_mW^T_qW_kp_n \end{aligned}\]

이 수식이, 대부분의 APE가 계산되는 과정이다. 저자들은 위 수식을 바꾸어 아래와 같이 만들었다.

\[q_m^Tk_n = x_m^TW_q^TW_kx_n + x_m^TW_q^T\widetilde{W}_k\tilde{p}_{m-n} + u^TW_kx_n + v^T\widetilde{W}_k\tilde{p}_{m-n}\]

여기서, 앞에서 각 항들을 앞에서 부터 (a),(b),(c),(d) 항이라고 할 때, 각 항은 아래와 같은 역할을 수행한다.
(a)항은 content만 사용되어 content-based addressing을 수행한다.
(b)항은 query의 content와 key의 position이 사용하여 content-dependent positional bias 역할을 수행한다.
(c)항은 query의 position과 key의 content를 사용하여 global content bias를 담당한다.
(d)항은 query와 key의 position을 사용하여 global positional bias 역할을 수행한다.

먼저, key에 대한 absolute positional vector 였던, $p_{n}$ 을 $\tilde{p}{m-n}$ 으로 바꾸어, 상대적인 위치를 주입했다. 여기서, $\tilde{p}{m-n}$ 는 sinusodial embedding을 사용하였다. (b,d)항

또한, 기존의 query에 대한 고정된 positional vector 였던, $p^T_{m}W_q^T$ 을 $u,v\in\mathbb{R}^d$ 로 변경하였다. 이는, query 에 대한 positional vector를 학습 가능하게 바꾸면서, 모든 위치에서 동일하게 만들어 위치에 독립적이게 바꾸었다.

마지막으로, 기존에 사용되던 Key에 대한 Weight Matrix를 content-based ( $W_k$ )와 location-based ( $\widetilde{W}_k$ )로 세분화하여, (a,c)항에는 content-based weight를, (b,d)항에는 location-based weight를 사용하였다.

Text-to-Text Transfer Transformer (T5)

과거의 시도들은, 대부분 positional vector를 Query와 Key에 대해 더해서 사용하였다. 이 부분을 자세히 살펴보자.

우리의 Transformer에서는 대게 다음과 같은 차원을 가지게 된다.
Key : (Batch,Head,Query,Dimension)
Query : (Batch,Head,Key,Dimension)

일반적으로, positional vector 또한 해당 Key,Query와 같은 차원의 matrix를 추가로 필요로 하게 된다. 대부분의 Transformer에서 Dimension은 768,1024 등 큰 규모의 숫자를 사용하는 것을 보았을 때, 적은 parameter가 아님을 짐작할 수 있다.

해당 방법을 learnable 방식으로 구현하게 될 경우, d-차원의 positional vector를 생성하기 위한 embedding lookup table이 추가로 필요하게 되며, 이는 계산 및 메모리 비용의 증가를 초래한다.
그렇다고, sinusodial 방법을 사용하기에는, 위의 sinusodial APE에서 다루었듯이 표현력에서 문제가 발생할 수 있다.

그래서, 저자들은, 이런 생각을 했을 것이다.

d-dimensional position vector를 사용하는게 아니라, 단순히 단일 scalar를 더해주므로써, 정보를 주입할 수 있지 않을까?

그 방법에서 나온 것이 아래와 같은 식이다.

\[q_m^Tk_n = x_m^TW_q^TW_kx_n + b_{i,j}\]

이렇게 보면, 위의 것과 차이가 크지 않아 보일 수 있다. 그러나 이를 자세히 보면, 단순히 token embedding에 대해 Key와 Query를 내적하고, 그것에 scalar를 더한 구조라는 것을 알 수 있게 될 것이다.

그렇다면, 우리는 다음 차원의 matrix만 만들면 positional information을 주입할 수 있다.

scores = <Query,Key> = (Batch,Head,Input Sequence Length,Key Length)

이는, 위의 Position Embedding들에 비해 메모리와 계산을 크게 절약할 수 있는 방법이다.

또한, 논문의 저자들은 “bucket”이라는 개념을 사용하였는데, 이는 계산에 효율성과 일반화에 도움이 되었다. 전체 상대적인 구간을 가까운 정보를 포함하고 있는 “exact” bucket과 먼 거리의 정보를 rough하게 포함하고 있는 “log” bucket을 사용하였다.

그러나, APE 식의 중간의 content와 bias가 섞인 부분에서 absolute position과 단어 사이의 연관성이 발견되어, 아래와 같이 다른 projection matrix에 position 이나 word 등을 추가하였다.

\[q_m^Tk_n = x_m^TW_q^TW_kx_n + p_m^TU^T_qU_kp_n + b_{i,j}\]

그러나, 실제 구현을 살펴보니 projection matrix를 통한 추가는 구현되어있지 않았다. [github]

DeBERTa: Decoding-enhanced BERT with Disentangled Attention

이 논문은, APE 식의 중간의 content와 bias가 섞인 부분을 사용해야지만, 완전히 모델링할 수 있다고 주장하며, 기존 APE의 식에서 $p_m,p_n$ 을 $\tilde{p}_{m-n}$ 으로 바꾸었다.

\[q_m^Tk_n = x_m^TW_q^TW_kx_n + x_m^TW_q^TW_k\tilde{p}_{m-n} + \tilde{p}^T_{m-n}W_q^TW_kx_n\]

Idea

위와 같이, Relative Position Embedding은 위치 정보를 주입하기에 좋은 방법으로 보인다. 그러나, positional vector를 사용하는 것에는 큰 문제점이 있었는데, self-attention layer의 query-key에 대해 매번 positional vector를 추가해야하는 단점이 있다. 또한, 토큰을 생성할 때마다, 이전 토큰들과 비교를 해야하기에, positional vector를 구하는데 많은 비용이 든다.

또한, T5의 경우, 복잡한 상황을 단일 scalar로 표현하기에는 부족한 문제가 있었다.

그렇기에, 저자들은 positional vector를 따로 더하지 않으면서도, position에 해당하는 정보를 주입시키고자 하였다. 그렇기에, QK의 내적 형태를 유지하면서 상대 위치가 내적을 하면 자동적으로 나타나는 구조를 찾고자 하였다. 이를 수학적으로 표현하자면 아래와 같다.

\[\langle q_m,k_n \rangle = g(x_m,x_n,m-n)\]

을 만족하는 함수 g를 찾는 것이 목표였다.

Key Previous Papers

  • Transformer : Attention Is All You Need [PAPER]

Architecture

Rotary position embedding(RoPE) in 2D

저자들은, d = 2, 즉 2차원에서부터 내적을 하면 자동적으로 거리의 뺄셈과 같은 효과가 나타나는 방법을 찾기 시작하였다. 그 결과, Re[]은 복소수의 실수부, $(W_kx_n)^*$ 은 $(W_kx_n)$의 결레 복소수, $\theta \in \mathbb{R}$ 인 0이 아닌 constant일 때의 아래 식을 찾게 되었다.

\[\begin{aligned} q_m = (W_qx_m)e^{im\theta} \\ k_n = (W_kx_n)e^{in\theta} \\ \langle q_m,k_n \rangle = ((W_qx_m)e^{im\theta})((W_kx_n)e^{in\theta})^H \\ = (W_qx_m)(W_kx_n)^He^{im\theta}e^{-in\theta}\\ \therefore g(x_m,x_n,m-n) = Re[(W_qx_m)(W_kx_n)^*e^{i(m-n)\theta}] \end{aligned}\]

자, 이렇게 보다시피, 뒤에 $e^{im\theta}$ 항을 붙여준 것 만으로도, 복소수의 내적시 m-n의 상대 위치가 나오게 된다.

내적을 했는데, 켤레복소수가 나오는 이유에 대해서 궁금하다면, 이 포스트를 참고하라.

지금 이 문제는 2차원에 한정되어 있으므로, 다음과 같이 쓸 수 있다.

\[\begin{aligned} x_m = \begin{pmatrix} x_m^{(1)}\\ x_m^{(2)} \end{pmatrix} \in \mathbb{R}^{2} \\ W_q = \begin{pmatrix} W_q^{(11)} W_q^{(12)}\\ W_q^{(21)} W_q^{(22)} \end{pmatrix} \in \mathbb{R}^{2\times 2} \\ y := W_qx_m = \begin{pmatrix} W_q^{(11)}x^{(1)}_m+W_q^{(12)}x^{(2)}_m\\ W_q^{(21)}x^{(1)}_m+W_q^{(22)}x^{(2)}_m \end{pmatrix} := \begin{pmatrix} y^{(1)}\\ y^{(2)} \end{pmatrix} \in \mathbb{R}^2 \end{aligned}\]

그렇다면, y는 x의 선형 변환된 행렬이라고 볼 수 있을 것이다.

자, 근데 왜 저자들은 “Rotary”라는 말을 사용하였을까?
이미, 대부분의 독자들이 눈치챘겠지만, 아래와 같은 오일러 공식 때문이다.

\[e^{i\theta} = cos \theta + isin\theta\]

마음에 와닫지 않을 수 있다.

아래에 $ e^{i\theta} = cos \theta + isin\theta $ 를 행렬로 바꿔보면, 알 수 있다.

\[\begin{aligned} e^{i\theta} = cos \theta + isin\theta = \begin{pmatrix} cos\theta \quad -sin\theta\\ sin\theta \quad cos\theta\\ \end{pmatrix} \end{aligned}\]

어떻게, 있던 i가 사라지고 저렇게 삼각함수들만 남았나 궁금하다면, 이 포스트를 참고하라.

따라서, 우리는 이제 아래와 같이 쓸 수 있다.

\[\{q,k\}_m = \begin{pmatrix} cosm\theta \quad -sinm\theta\\ sinm\theta \quad cosm\theta\\ \end{pmatrix} \begin{pmatrix} W_{\{q,k\}}^{(11)} W_{\{q,k\}}^{(12)}\\ W_{\{q,k\}}^{(21)} W_{\{q,k\}}^{(22)} \end{pmatrix} \begin{pmatrix} x_m^{(1)}\\ x_m^{(2)} \end{pmatrix}\]

보라, 이는 회전변환 행렬이 생겼다! 따라서, 저자들은 이 방법에 “Rotary”라는 이름을 붙였을 것이다.

Rotary position embedding(RoPE) in General

우리는, 위에서 RoPE가 2D에서 잘 동작하는 것을 확인하였다. 그렇다면, 2D에서 식을 최대한 활용하기 위해 차원 d를 짝수라고 가정하였고, 그 후에 $\forall x_i \in \mathbb{R}^d$ 를 d/2개의 sub-space로 분할하고, 내적의 선형성을 이용하여 sub-space를 결합하였다. 그렇다면, 다음과 같은 구조를 가지게 될 것이다.

\[\begin{aligned} \{q,k\}_m=R^d_{\Theta,m}W_{\{q,k\}}x_m, \\ R_{\Theta,m}^{d}= \begin{pmatrix} \cos m\theta_{1} & -\sin m\theta_{1} & 0 & 0 & \cdots & 0 & 0 \\ \sin m\theta_{1} & \cos m\theta_{1} & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m\theta_{2} & -\sin m\theta_{2} & \cdots & 0 & 0 \\ 0 & 0 & \sin m\theta_{2} & \cos m\theta_{2} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2} & -\sin m\theta_{d/2} \\ 0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2} & \cos m\theta_{d/2} \end{pmatrix}\\ \Theta = \{\theta _{i} = 10000^{-2(i-1)/d},i\in [1,2,\cdots,d/2]\} \\ \therefore q^T_mk_n = (R^d_{\Theta,m}W_qx_m)^T(R^d_{\Theta,n}W_kx_n) = x^TW_qR^d_{\Theta,n-m}W_kx_n \end{aligned}\]

Graphical explanation of RoPE

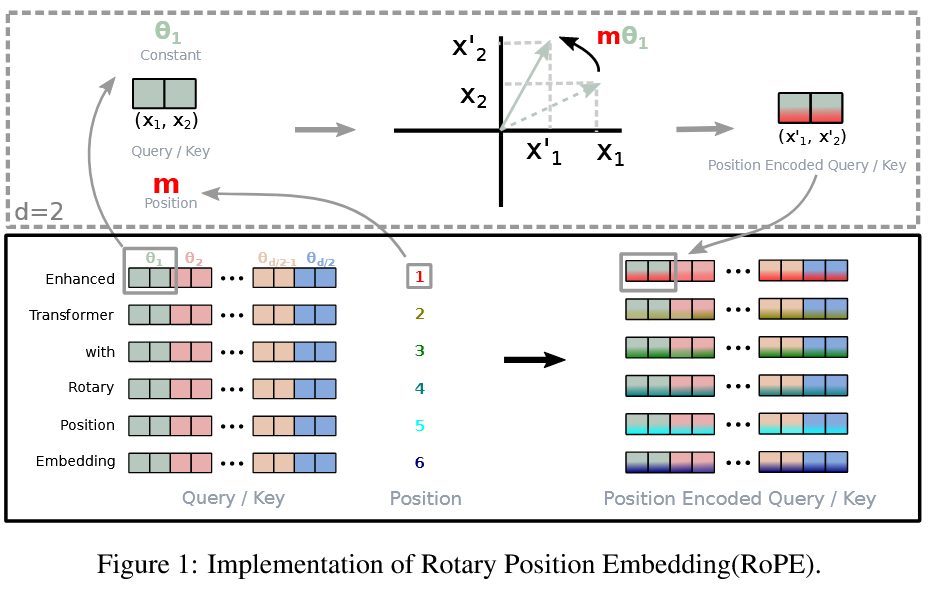
위의 그림은, RoPE를 Graphical하게 설명한 그림이다. 같이 이해해보도록 하자.

\[\begin{aligned} \text{Let Token Embedding Vector } x \in \mathbb{R}^d, \\ x = (x_1,x_2,\cdots,x_d), \quad i\in \{1,2,\cdots,d\}. \\ \theta _n = (x_{2n-1},x_{2n}), \quad n\in \{1,2,\cdots,d\} \end{aligned}\]

와 같이 표현할 수 있다. 이러한 상황에서 Key와 Query에 대해서 위치 m에서, $e^{im\theta}$ 를 곱해주어, $m\theta$ 만큼 원래의 Key, Query를 회전시키는 것이다.

하지만, 위의 회전은, d차원의 모든 회전을 나타낼 수는 없다. Block-diagonal rotation이기 때문이다. 따라서, 회전을 $R$ 이라고 할때, 아래와 같은 제약이 존재한다.

  • $R:\mathbb{R}^d \to \mathbb{R}^d,\quad V \le \mathbb{R}^d, \qquad V \text{ is } R\text{-invariant} \;\Longleftrightarrow\; R(V)\subseteq V.$ (invariant)
  • $V_i := \mathrm{span}(e_{2i-1},e_{2i}), \quad i=1,\dots,\left\lfloor \frac{d}{2}\right\rfloor. \qquad \forall i,\; R(V_i)\subseteq V_i.$ (not mixing)

그렇다면 왜, 저자들은 전체 embedding vector $x$ 를 회전시키는 것이 아닌, 일부를 잘라서 다음과 같이 블록대각형태를 만들어 회전시켜야만 했던 것일까? 사실 저자들은 이유를 적어두지는 않았다. 그러나, 내가 추측컨데, 2D 회전은 각도 하나로 매우 간단히 파라미터화되지만, d차원에서는 아니여서 그렇다. 따라서 저자들은 계산 및 최적화 안정성을 위해 임베딩 차원을 2차원 블록으로 분할하고, 각 블록에서 독립적인 2D 회전을 수행하는 block-diagonal rotation을 선택한 것으로 추측된다.

You may also enjoy