About Problem to solve

Idea

모델의 Generalization ability는 모두가 동의하듯이 중요하다. 이에, text-to-text 분야에서는 autoregressive(GPT) 또는 masked language modeling(BERT) 등의 방법론을 많은 데이터에 대해 사용하면, 학습을 하지 않은 데이터셋에서도 준수한 성능을 보이고 있다. (Zero-shot ability). 여기서 집중해야하는 것은 많은 데이터로, Web에서 수집된 대규모 데이터셋은 소규모의 고품질 라벨링 데이터셋보다 더 효과적인 supervision signal을 제공할 수 있다는 것을 GPT와 같은 LLMs(Large Language Models)의 성공이 시사한다.

그렇다면, ImageNet으로 Pretraining하는 것이 관행인 CV (Computer Vision)분야에서도 위와 같은 대용량 데이터셋을 사용하면 좋지 않을까?

Key Previous Papers

  • conVIRT : Contrastive Learning of Medical Visual Representations from Paired Images and Text, 265K image-text pair [Paper]
  • ICMLM : Learning visual representations with caption annotations, 231K image-text pair [Paper]
  • VirTex : Learning visual representations from textual annotations [Paper]
  • SimCLR : A Simple Framework for Contrastive Learning of Visual Representations [Paper]

    Methodology

    Data preparation

    400M Image-Text Paired Dataset

Text 선정 : Wikipedia에서 최소 100번 쓰인 단어. => 500,000 quries
각각의 qurey는 최대 2만 개의 (image,text) pair를 포함하도록 구성되어 있음. => WebImageText

Model structure

400M의 dataset을 무작정 학습시키는 것은, 너무 오랜 시간을 필요로 한다.

저자들은, 초기의 시도로, VirTex와 같이 image의 CNN과 text의 Transfomer를 함께 학습시켜 image의 Caption을 예측하도록 모델을 훈련시켰다. 그러나, 동일한 (image,text) pair에 대해 입력받은 image에 대해 text를 bag-of-words 방식으로 인코딩하여 예측하도록 하는 간단한 BASELINE 모델보다 3배 느렸다.

저자들은, 문제의 이유를 정확한 단어를 예측하려고 하는데 있다고 생각하였다.
모델은, 정확한 단어를 예측하도록 설계되어 있지만, 이미지와 함께 등장하는 설명 등 관련 텍스트는 다양하기에, 본질적 모델의 설계 철학이 맞지 않다는 것이다.

그렇다면, 정확한 단어를 **예측**하지 않으면 되지 않는가?

그래서, 저자들은 기존 BASELINE에서 예측을 하고자 사용했던 loss를, Contrastive loss로 변경하였더니, 4배 효율적이 되었다!

그렇다면, 조금더 디테일하게 모델을 어떻게 변경하였을까?

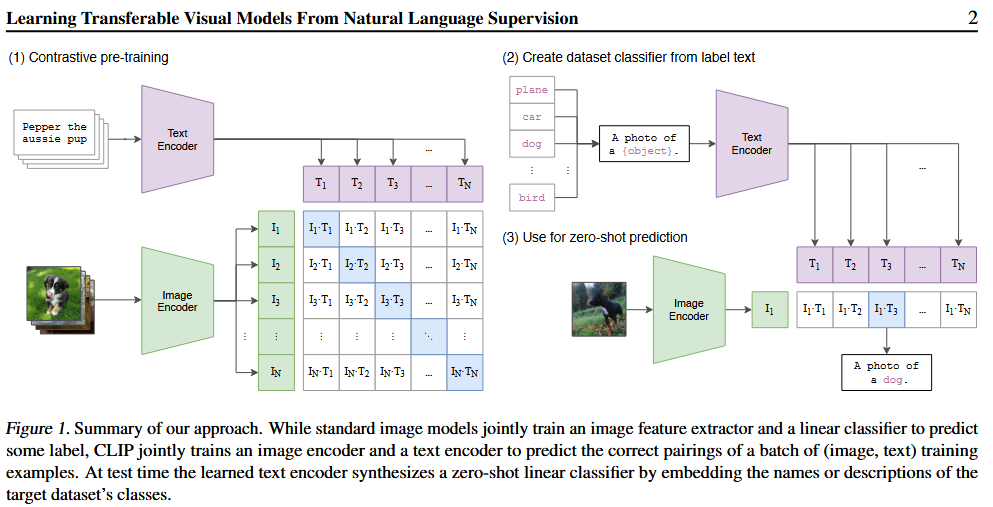
위의 그림과 같이 N개의 image와 N개의 Text로 이루어진 $N^2$개의 image-text pair에 대해 아래와 같이 학습한다.

  • N개의 맞게 매치된 pair는 cosine similarity를 Maximize하는 방향으로 학습
  • 나머지 $N^2-N$개의 pair는 cosine similarity를 Minimize하는 방향으로 학습
  • 이렇게 구한 유사도 점수에 Symmetric cross-entropy loss 적용

또한, 논문에 명시된 것과 같이, CLIP의 구현은 다음과 같이 추상화 될 수 있다.

Numpy-liked implementation of CLIP

여기까지, 모든 내용을 이해했으면, 우리는 궁금증을 가져야 한다.

1. Negative pair (Incorrect matched $N^2-N$ pairs)에 대해 cosine similarity를 Maximize하는 Term은 어디에 있는가?
2. SimCLR 등으로 유명해진 representation과 Contrastive embedding space 사이의 non-linear projection를 추가하는 것은 왜 사용하지 않았는가?

Negative pair를 찾아서

Cross-entropy와 InfoNCE의 관계

이 답을 알기 위해서는, [InfoNCE]와 Cross-entropy에 대해서 알아야 한다.

일단, 우리가 Contrastive Learning에서 자주 사용하는 InfoNCE는 다음 수식과 같이 정의된다.

\[\mathcal{L}_N = - \mathbb{E}_{X} \left[ \log \frac{f_k(x_{t+k}, c_t)} {\sum_{x_j \in X} f_k(x_j, c_t)} \right]\]

위의 식은, set $X = {x_1, \cdot\cdot\cdot x_N }$ 과 of $N$ random sample 중 $p(x \mid c)$ 로 부터 추출된 1개의 positive sample과 ‘proposal’ distribution $p(x)$ 에서 추출된 N-1 negative sample에 대해서 성립한다.

\[f_k(x_{t+k}, c_t) \propto \frac{p(x_{t+k} \mid c_t)}{p(x_{x+k})}\]

그러나, 해당 논문은 t 시점에서 k-step 앞을 나타내는 시계열을 기반으로 작성되었기에, 우리는 k와 t를 제거하고 다음과 같이 사용할 수 있다.

\[\mathcal{L}_N = - \mathbb{E}_{X} \left[ \log \frac{f(x^{+}, c)} {\sum_{x_j \in X} f(x_j, c)} \right]\]

또한, $f(x, c) $는 구현 상에서 $exp(sim(x,c))$로 구현되기에, 우리는 다시 정리하여

\[\mathcal{L}_N = - \mathbb{E}_{X} \left[ \log \frac{exp(sim(x^+,c))} {\sum_{x_j \in X} exp(sim((x_j, c)))} \right] \rightarrow \ell = -\log \frac{exp(sim(x^+,c))} {\sum_{x_j \in X} exp(sim((x_j, c)))}\]

가 된다. 그렇다. 우리는 이것을 어딘가에서 많이 봤을 것이다. Cross-entropy에 Softmax를 취한, 우리가 흔히 nn.Softmax()로 사용하는 구현체와 유사하게 나오게 되며, 아래의 SimCLR paper에서 본 로스와 $\tau$를 제외하면 같아진다.

\[\ell_{i,j} = - \log \frac{ \exp\left(\mathrm{sim}(z_i, z_j)/\tau\right) }{ \sum_{k=1}^{2N} \mathbb{1}_{[k \neq i]} \exp\left(\mathrm{sim}(z_i, z_k)/\tau\right) }\]

위의 Numpy-liked pseudo code를 자세히 살펴보면, label은 np.arange(n) 정답 클래스를 만들었고, CE 내부적으로 다음과 같이 one-hot encoding 되듯이 해석된다.

\[y_{ij} = \begin{cases} 1 & \text{if } j = \mathrm{labels}[i] = i \\ 0 & \text{if } j \neq i \end{cases}\]

그렇다면, 정답 pair가 아닌 곳은 0이 되므로, 분자의 기여하지 않게된다. 즉 아래와 같이 되는 것이다.

\[- \log \frac{ \exp\left(z_{ii}\right) }{ \sum_{k} \exp\left(z_{ik}\right) }\]

InfoNCE에서의 negative pair

자, 그러면 우리는, CLIP에서 구현한 loss가 InfoNCE의 그것과 거의 같은 식이라는 것을 이해하였다. 그러면 우리는 위의 문제의 답을 찾을 수 있다.
사실, 우리의 loss는 negative term 또한 Minimize하고 있다.
단지, positive pair의 similarity를 negative pair의 similarity대비 최소화하는 것이, 해당 loss의 목표이다. 이는 우리가 부르는 implicit repulsive force라고 부르는 것이다.

non-linear projection을 사용하지 않은 이유.

사실, 위의 negative term에 대한 설명에 비해, 간단한 이유를 가지고 있다.
그냥 성능이 늘지 않았다.
그래서, 저자들은 해당 non-linear projection이 image single-modal에 co-adaptation되었을 수 있다고 추측한다.

Pros of paper

  1. 유연한 Zero-shot 전이 능력 (Text-to-Image retrieval 등)
  2. 정형화된 label을 사용하는 것이 아닌, 자연어를 파악하기에, 확장성이 높음. (인터넷에 존재하는 텍스트-이미지를 사용할 수 있음)

Cons of paper

  1. Negative loss를 명시적으로 사용하지 않았고, SimCLR과 같이 batch size에 영향을 받을 수 밖에 없는 구조를 사용하였다.

읽고 난 후의 질문

  1. 과연 진정으로, non-linear projection을 하였을 때, 성능이 좋지 않았을까? 설계의 한계가 있지 않았을까? 왜냐하면 Intermediate layer의 potential이 있다는 논문을 보았기 때문이다. [PAPER]

You may also enjoy